| Autophagy dynamics at the level of a single cell |
| This research is a collaboration
between Los Alamos Laboratory (Bill Hlavacek, Yen-Ting Song, Song Chen)
and UNM (Francesco Sorrentino, Afroza Shirin, Isaac Klickstein). |
| |
| Autophagy is a cellular housekeeping and digestive process where misfolded or aggregated proteins,
damaged organelles, and intracellular pathogens are identified by the cell, trapped in double-membrane
vesicles, called autophagosome vesicles (AVs), and then delivered to the lysosome in the cell for degradation. Autophagy is also induced in conditions of nutrient starvation, during which it provides cells with
additional nutrient supplies. |
| |
| The motivating consideration for mechanistically investigating how to optimize the level of autophagy
is to better understand cell survival and death. Autophagy, as a mechanism for cell survival, can promote
the growth of established tumors and increase their resistance to treatments [1, 2, 3, 4]. Therefore, efforts
to inhibit autophagy to improve cancer therapy are a critical next step. |
| |
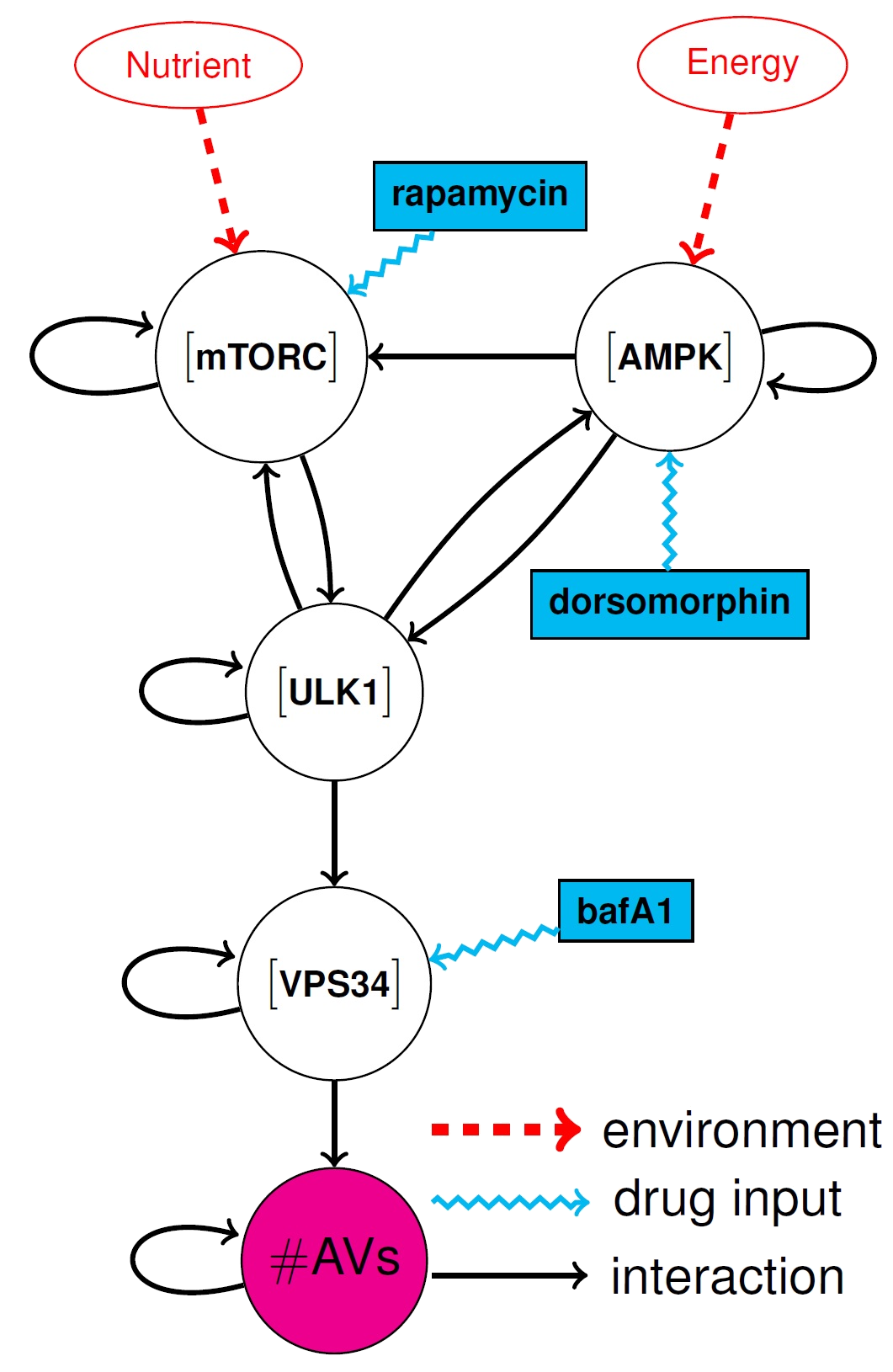
| We attempt to control the number of AVs in a cell by supplying different types of pharmacological
reagents (PRs). With the help of our collaborators at Los Alamos, we have developed a simplified 5-dimensional dynamical model, which is schematically represented in the
figure and is described by the
following set of ODEs: |
| |
 = (1-x_1)g_1 (1 - u_1) (1 - u_2)- x_1 h(x_2) h(x_3)) |
![x_1: $[mTORC]$](http://latex.codecogs.com/gif.latex?x_1: $[mTORC]$) |
 = (1-x_2) h(x_3) (1 - u_3) -x_2 h(x_1)) |
![x_2: $[ULK1]$](http://latex.codecogs.com/gif.latex?x_2: $[ULK1]$) |
 = (1-x_3)k_1 (1 - u_4) - g_2 x_3 x_2 (1 - u_5)) |
![x_3: $[AMPK]$](http://latex.codecogs.com/gif.latex?x_3: $[AMPK]$) (1) (1) |
 = (1-x_4)k_2 h(x_2) - k_3 x_4) |
![x_4: $[Vps34]$](http://latex.codecogs.com/gif.latex?x_4: $[Vps34]$) |
 = k_4 x_4 - k_5 x_5 (1- u_6)) |
 |
| |
subject to the following (possible) control inputs/PRs: 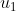 : Rapamycin : Rapamycin 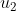 : Taselisib; : Taselisib; 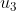 :
Sbi0206965; :
Sbi0206965;  : Dorsomorphin; : Dorsomorphin;  : A769662; : A769662;  : Bafa1. : Bafa1.
|
| |
In Eq. (1) the  = \frac{6 x_i^{n_i}}{x_i^{n_i}+\vartheta_i^{n_i}}) are scaled Hill functions,
where are scaled Hill functions,
where 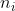 is an even integer and is an even integer and  is a constant for each is a constant for each  are the rate constants;
are the rate constants; 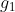 and and  are the amount of nutrients and energy available in a cell.
Nutrients are building blocks of proteins, amino acids, and nucleotides.
Energy is provided by Adenosine triphosphate (ATP) molecules.
When these two constants are changed we see qualitative changes of the dynamics
[5]. are the amount of nutrients and energy available in a cell.
Nutrients are building blocks of proteins, amino acids, and nucleotides.
Energy is provided by Adenosine triphosphate (ATP) molecules.
When these two constants are changed we see qualitative changes of the dynamics
[5]. |
| |
This model is derived from a higher-dimensional model for autophagy regulation
[5, 6] that will be used to validate the control solution derived for the
low dimensional model.
The figure is a network representation for the system of equations (1), where each node corresponds to one of the
states of the system and a directed edge connects node  to node to node  if
if  appears in the equation for the time evolution of appears in the equation for the time evolution of  . . |
| |
 |
| |
| The goal is to affect the number of AVs (target) by injecting selected control inputs/PRs into
certain network nodes. Recent studies (see e.g. [7, 8, 9, 10]) have identified several proposed strategies for autophagy inhibition.
These involve different PRs. Among these: (1) {Rapamycin} (an mTORC kinase inhibitor) prevents cell growth;
(2) Bafa1 (a VPS34-complex inhibitor) impairs phagophore (the isolation membrane that delimits the part of cytoplasm that the cell eats)
nucleation and (3) {Dorsomorphin} (an AMPK inhibitor) blocks cellular energy homeostasis. These three PRs are shown in blue in the figure,
affecting three different nodes, i.e., `a cocktail of drugs'. Note that Eq. 1 is more general and considers a total of 5 possible PRs,
which provides the possibility for many more PR combinations. |
| |
| This research incorporates a novel approach as it includes a comparison of several
strategies in terms of controllability and control energy (amounts of drug needed and its dosage over time).
The timescale for autophagy dynamics is on the order of hours [6].
Here we assume to be able to affect the system with control inputs (PRs) that evolve on a timescale
comparable with that of the system's dynamics. The control strategy is open loop, as real-time information
on the time-evolution of the activity of a cell is typically unavailable. |
| |
| We have computed optimal control trajectories that provide optimal dosage functions for several PRs.
The results of some of our computations are shown below for Rapamycin, ...
|
| |
In our simulations, we set the initial condition for each state to be equal to the steady state solution
for the system of Eqs. (1) in free evolution (i.e., when =0, i=1,...,6) ) and set the amount of nutrition and energy ) and set the amount of nutrition and energy
 . The goal of the control action is to
upregulate/downregulate the final number of autophagy vesicles
at the end of a fixed time period . The goal of the control action is to
upregulate/downregulate the final number of autophagy vesicles
at the end of a fixed time period ) , while minimizing the control effort, i.e., the overall quantity of each drug that is provided during the time period.
The motivation for this choice of the objective function is to use the least quantity of a drug and to reduce unwanted off-target effects. The chosen control timescale $t_f$ is
consistent with experimental observations for the time that it takes for autophagosomes to form in a cell [6]. In each of the figures below, panel (c) shows a curve of the minimum control
energy versus the target quantity of AVs. These curves show how changing the final requirements in terms of target AVs affects the minimum required expenditure of each individual drug. , while minimizing the control effort, i.e., the overall quantity of each drug that is provided during the time period.
The motivation for this choice of the objective function is to use the least quantity of a drug and to reduce unwanted off-target effects. The chosen control timescale $t_f$ is
consistent with experimental observations for the time that it takes for autophagosomes to form in a cell [6]. In each of the figures below, panel (c) shows a curve of the minimum control
energy versus the target quantity of AVs. These curves show how changing the final requirements in terms of target AVs affects the minimum required expenditure of each individual drug.
|
| |
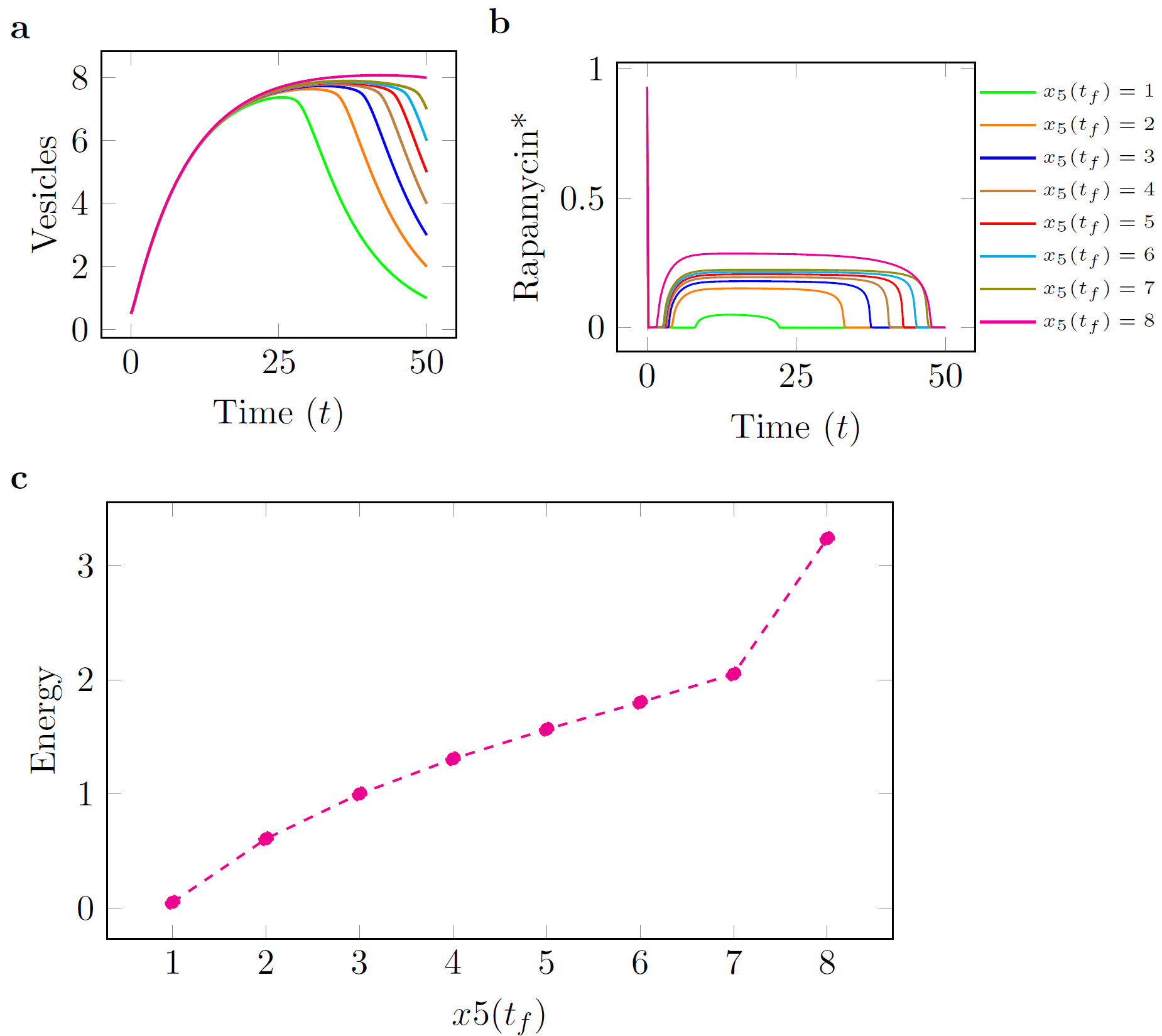 |
| Figure: Rapamycin
|
| |
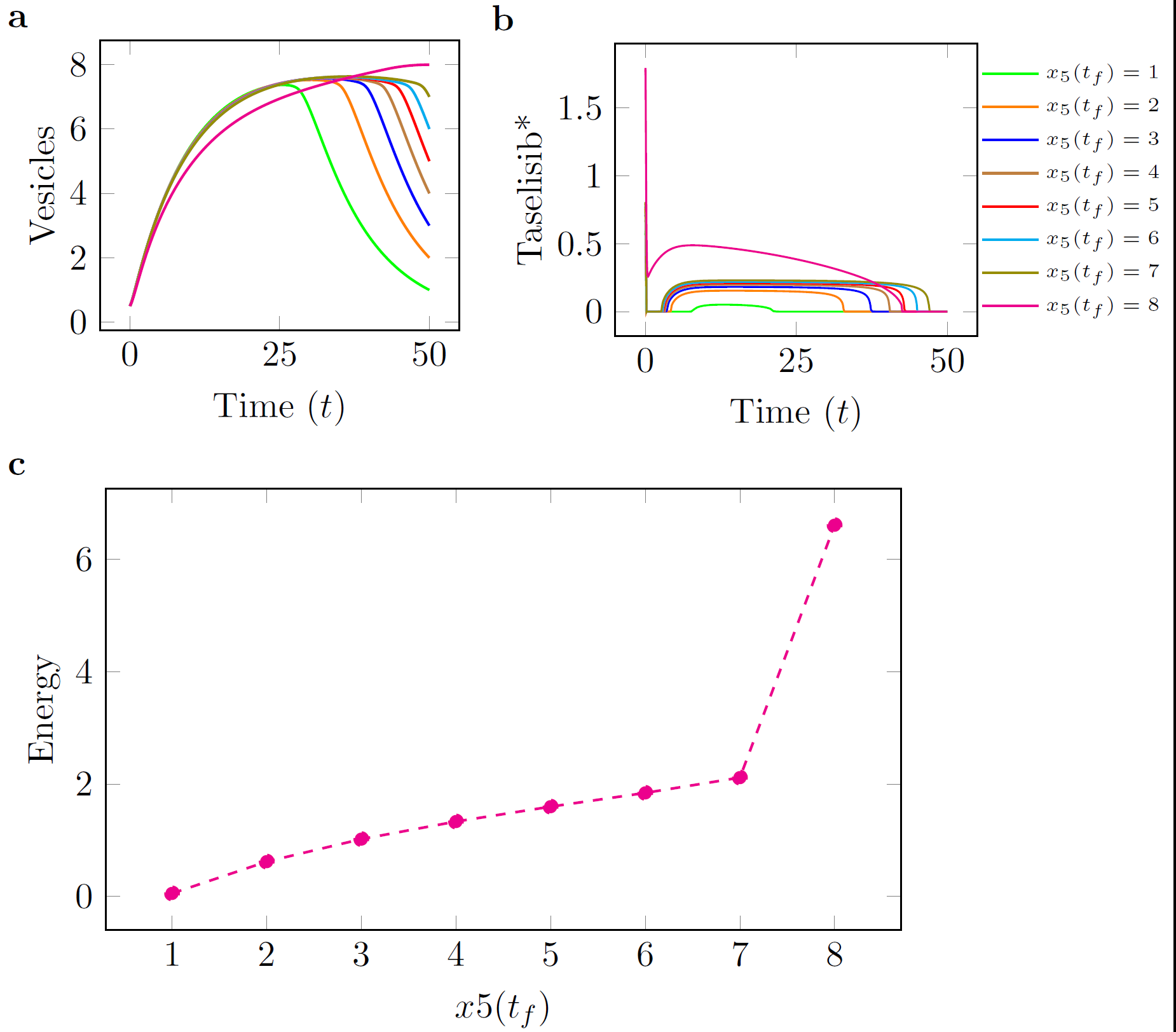 |
| Figure: Taselisib
|
| |
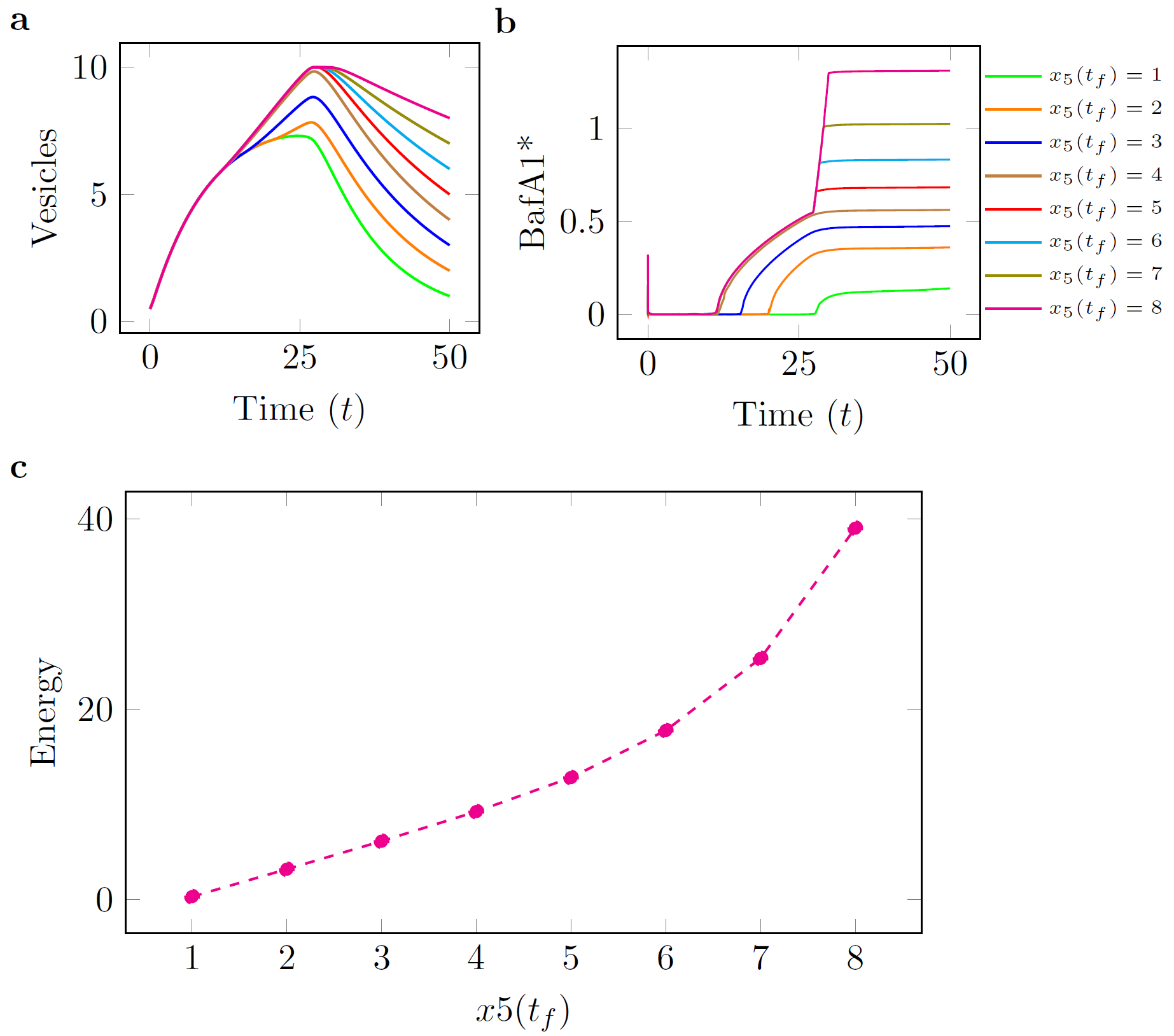 |
| Figure: BafA1
|
| References |
| [1] Zhineng J Yang, Cheng E Chee, Shengbing Huang, and Frank A Sinicrope. The role of autophagy in cancer: therapeutic implications. Molecular cancer therapeutics, 2011. |
| [2] Hsin-Yi Chen and Eileen White. Role of autophagy in cancer prevention. Cancer Prevention Research, 2011. |
| [3] Eileen White. The role for autophagy in cancer. The Journal of clinical investigation, 2015.
|
| [4] Angeleen Fleming, Takeshi Noda, Tamotsu Yoshimori, and David C Rubinsztein. Chemical modu- lators of autophagy as biological probes and potential therapeutics. Nature chemical biology, 2011.
|
| [5] Paulina Szymanska, Katie R Martin, Je rey P MacKeigan, William S Hlavacek, and Tomasz Lip- niacki. Computational analysis of an autophagy/translation switch based on mutual inhibition of mtorc1 and ulk1. PloS one, 10(3):e0116550, 2015. |
| [6] Katie R Martin, Dipak Barua, Audra L Kau man, Laura M Westrate, Richard G Posner, William S Hlavacek, and Je rey P MacKeigan. Computational model for autophagic vesicle dynamics in single cells. Autophagy, 2013. |
| [7] Guido Kroemer and Beth Levine. Autophagic cell death: the story of a misnomer. Nature reviews Molecular cell biology, 9(12):1004{1010, 2008. |
| [8] Ravi K Amaravadi, Duonan Yu, Julian J Lum, Thi Bui, Maria A Christophorou, Gerard I Evan, An- drei Thomas-Tikhonenko, and Craig B Thompson. Autophagy inhibition enhances therapy-induced apoptosis in a myc-induced model of lymphoma. Journal of Clinical Investigation, 117(2):326, 2007. |
| [9] Viktor I Korolchuk, Alicia Mansilla, Fiona M Menzies, and David C Rubinsztein. Autophagy inhibi- tion compromises degradation of ubiquitin-proteasome pathway substrates. Molecular cell, 33(4):517{ 527, 2009. |
| [10] Kewei Wang. Molecular mechanism of hepatic steatosis: pathophysiological role of autophagy. Expert reviews in molecular medicine, 18, 2016. |
| |
| |





