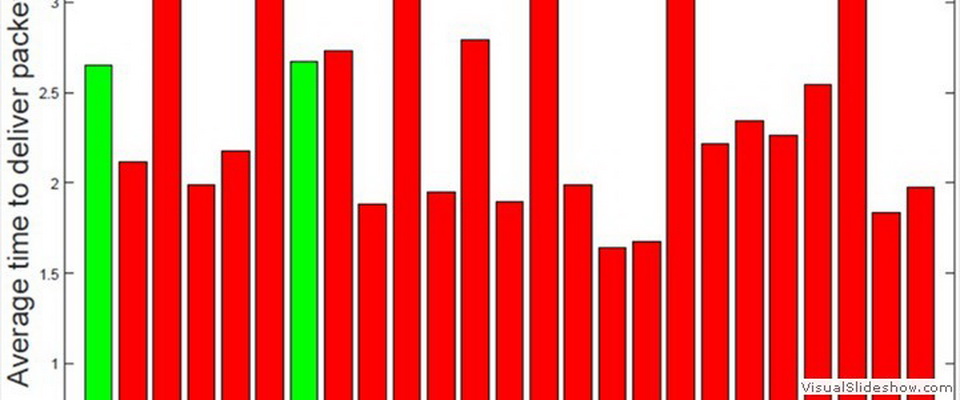
| Master Stability Functions | |
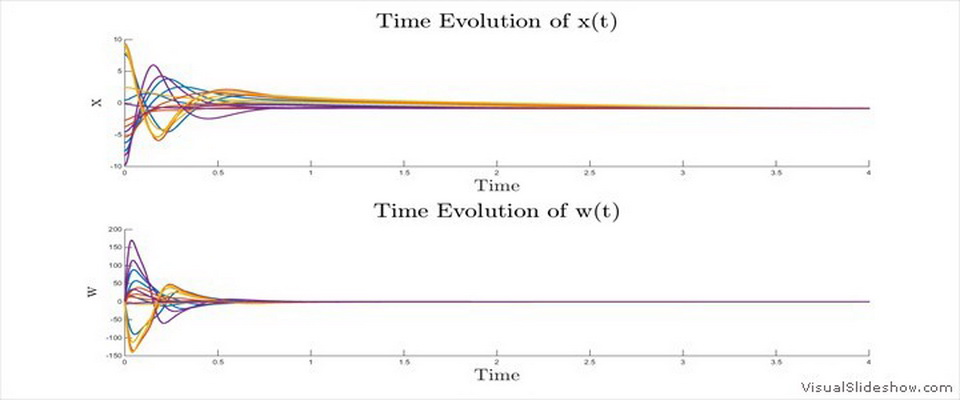
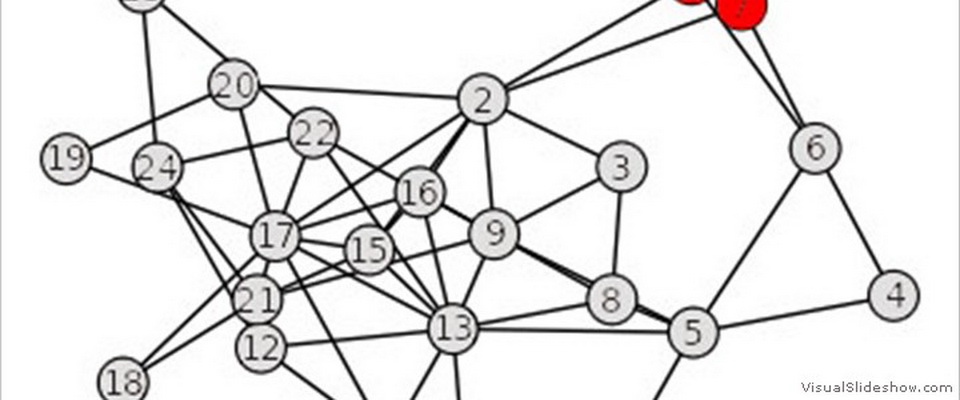
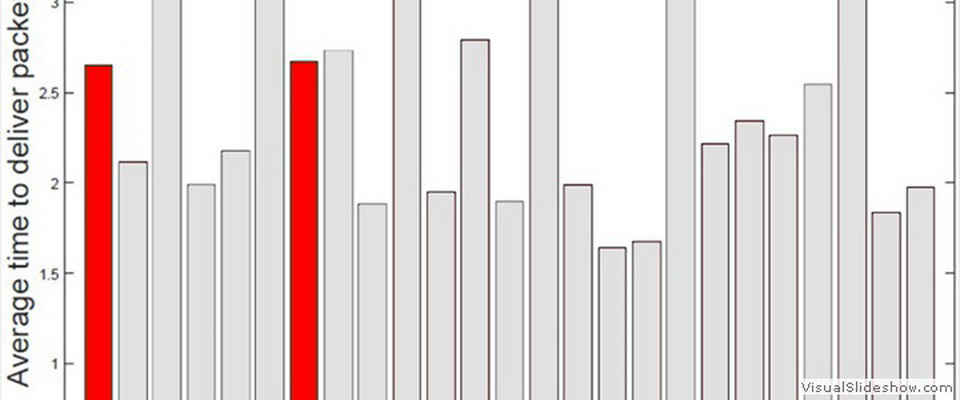
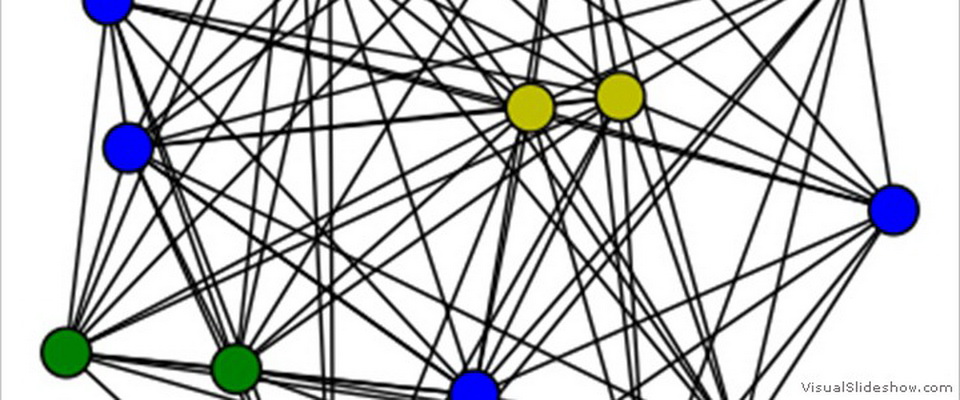
| Consider a network of coupled identical or quasi-identical dynamical systems that seek to synchronize. Master stability functions are powerful mathematical tools that provide necessary and sufficient conditions for stability of the synchronous solution. Usually, a master stability function refers to a low-dimensional system whose stability is associated with that of the original high-dimensional network. Obtaining such a reduction is often quite difficult, thus can be a reason of great satisfaction for the scientist who succeeds in the task. I have worked in this area and obtained 5 different reductions in a master stability function form for different problems related to synchronization of networks. I list them below. | |
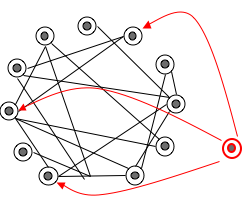 |
Pinning control of networks. |
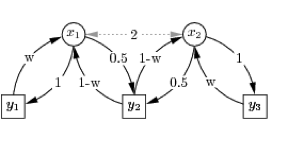 |
Network Synchronization of Groups. |
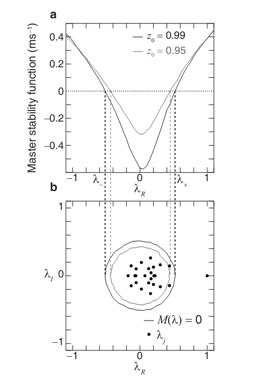 |
Adaptive synchronization of a time-evolving dynamical networks. |
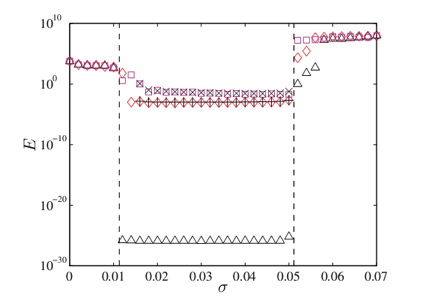 |
Networks of coupled dynamical systems characterized by a broad range of deviations from nominal conditions, i.e., small deviations in the dynamics of the individual units, in the output functions of the individual units, and in the coupling among the systems. |
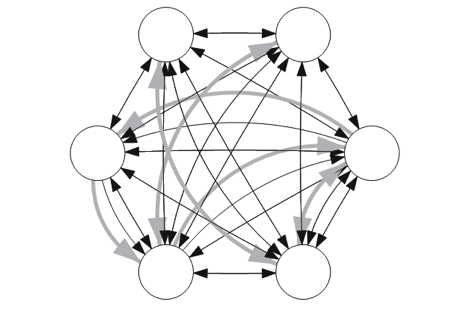 |
Hypernetworks of coupled dynamical systems. |
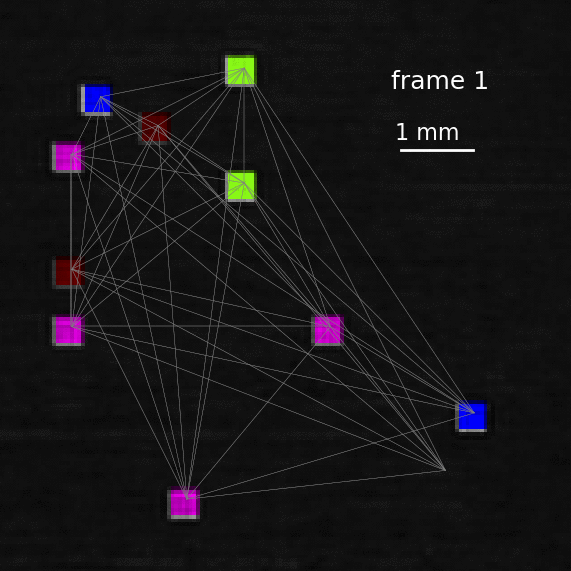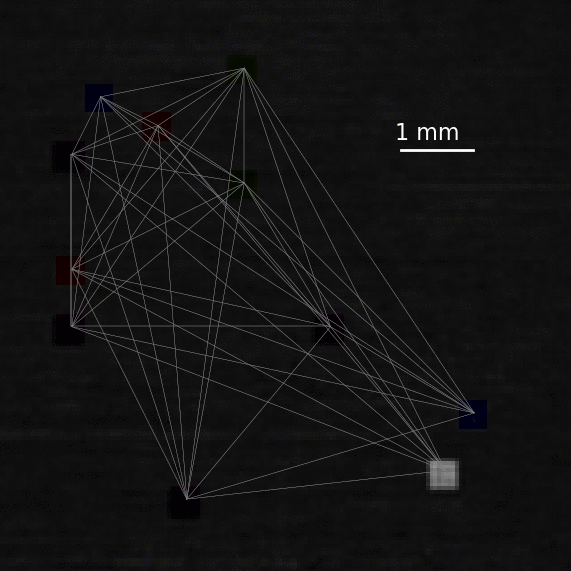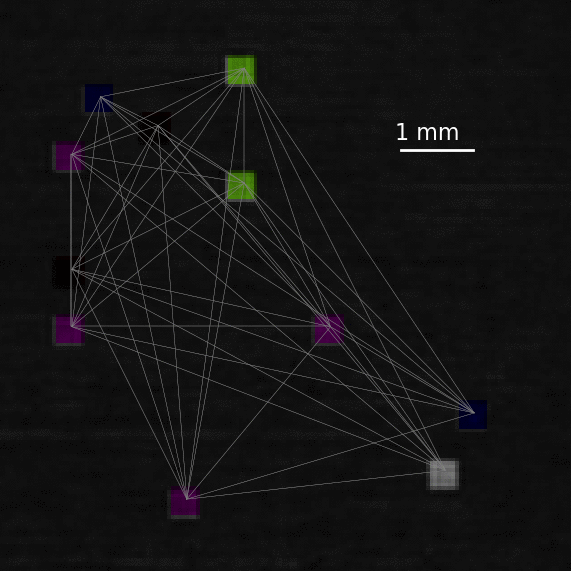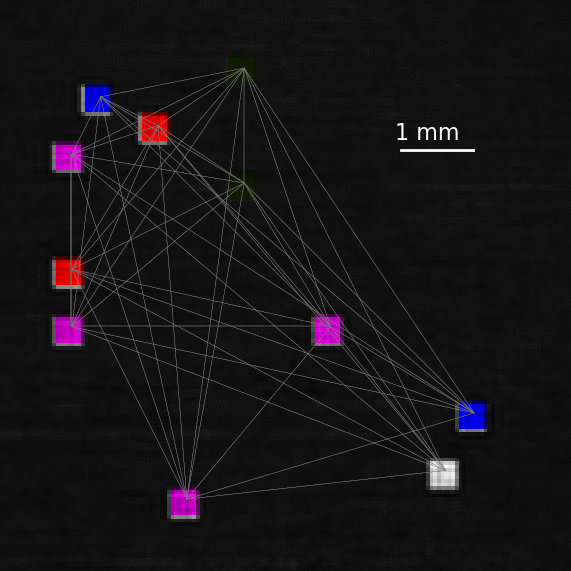 |
Cluster synchronization In networks with symmetries. |